Una de Encuestas Electorales
Introducción al diseño y análisis de encuestas electorales
Virgilio Gómez Rubio
Departamento de Matemáticas
Universidad de Castilla-La Mancha
Campus de Albacete
Introducción
Aprovechando que este jueves tengo clase con los alumnos de la Escuela de Mayores José Saramago de la UCLM sobre encuestas electorales, he decidido escribir una pequeña introducción al tema sin muchos detalles matemáticos. En este artículo me centraré en las elecciones municipales en Albacete celebradas el pasado 24 de mayo de 2015. En cualquier caso, la metodología es extrapolable a situaciones similares.
El objetivo de las encuestas electorales es hacer una estimación del porcentaje final de votos antes de que tengan lugar las elecciones. En general, el procedimiento es simple: se selecciona un conjunto de futuros votantes a los que se les pregunta sobre su intención de voto y se asume que la distribución del voto en estas encuestas se parecerá a los resultados reales. El resultado será más fiable cuanto mayor sea el número de votantes a los que se pregunte y, sobre todo, si esas personas representan de manera fiable al conjunto de los votantes de la ciudad de Albacete.
Formalizando el problema, nuestro interés es estimar la proporción de votos que obtendrán los principales partidos y, posiblemente, el porcentaje de votos a otros partidos y en blanco. Para las elecciones municipales en Albacete seleccionamos a PP, PSOE, Ciudadanos, Ganemos y UpyD por ser los partidos con más posibilidades en el momento de hacer las encuestas. La distribución de escaños se realiza solamente sobre los votos válidos, así que el porcentaje de votos nulos se suele ignorar, así como la abstención.
Selección de la muestra
Estadísticamente hablando, al conjunto de personas a las que hacemos las encuestas se conoce como muestra y al total de electores como población de estudio Lo que pretendemos es usar esa muestra para poder sacar conclusiones fiables de la población de estudio. Aunque generalmente cuanto mayor sea el tamaño de la muestra (es decir, el número de personas entrevistadas) mejores estimaciones obtendremos, hay una serie de consideraciones a tener en cuenta para que los resultados sean fiables:
- La muestra ha de ser representativa de la población, es decir, que debe incluir electores de varias edades, sexos, nivel de estudios, etc.
- Esto incluye realizar encuestas a personas de todos los barrios de Albacete
Cuando se diseña una encuesta se suele dividir a la población en grupos (o estratos) de acuerdo a una serie de variables socieconómicas y se selecciona un número de encuestas para cada uno de estos grupos. Esto se conoce como muestreo estratificado y suele ser mejor que seleccionar al azar una muestra de entre toda la población porque tiene en cuenta la estructura de la población. Por ejemplo, si el número de electores entre los 18 y 30 años es menor que el de mayores de 65 años, el muestreo debería recoger más encuentas de este último grupo de edad para ser representativo de la población. Si durante la recogida de datos esto no ha sido así, se puede hacer una corrección en los resultados (lo que popularmente se llama cocina).
El tamaño de la muestra se suele tomar de manera que el error (estadístico) cometido en las estimaciones de voto sea pequeño. El problema más común es que no hay presupuesto para alcanzar el error deseado y lo que se hace es estimar el error cometido en función del tamaño muestral que tengamos.
Estimación de porcentajes
Supongamos por un momento que estamos considerando el caso en el que únicamente tenemos dos partidos, A y B, y que estamos intentando estimar la intención de voto. Podemos considerar que los porcentajes de voto reales son \(\pi_A\) y \(\pi_B\). Supongamos también que sólo se puede votar a estas dos opciones, de manera que \(\pi_A = 1 - \pi_B\).
Conviene comentar que este tipo de problemas se da con más frecuencia de lo que parece. En Medicina, por ejemplo, estas situaciones se dan cuando se prueba un nuevo medicamento y se estudia si el paciente mejora (A) o no mejora (B). En este contexto, \(\pi_A\) mide la eficacia del medicamento o la proporción de pacientes que mejoraría con ese tratamiento, mientras que \(\pi_B\) sería la proporción de pacientes que no mejoraría. Estas proporciones se estimarían mediante el desarrollo de un ensayo clínico en el que a un grupo de pacientes se les da el tratamiento bajo estudio y se recogen cuántos mejoran y cuántos no.
Volviendo al contexto electoral, si preguntamos a una persona elegida al azar de entre todos los votantes, la probabilidad de que nos diga que va a votar al partido A sería de \(\pi_A\). Si preguntamos a un número grande de personas, la proporción que nos haya dicho que votará al partido A, y que llamaremos \(\hat{\pi}_A\), se parecerá mucho al valor real de \(\pi_A\). De manera similar tendríamos la proporción observada de votantes del partidos B, \(\hat{\pi}_B\), se ha de parecer a \(\pi_B\).
Por ejemplo, si preguntamos a 100 personas y 63 nos dicen que votarán al partido A tendríamos una estimación de la proporción real de votantes igual a \(\hat{\pi}_A = 63/100 = 0.63\). Para el partido B la estimación sería \(\hat{\pi}_B = 37/100 = 0.37\), que se ha de parecer mucho a la proporción real de votantes del partido B.
Estas estimaciones serán más fiables cuanto mayor sea el número de personas que entrevistemos siempre y cuando la muestra sea representativa de toda la población. Además, si repitiésemos las encuestas tomando a otro grupo de 100 votantes, las proporciones estimadas seguramente varíen un poco, dependiendo del error que estemos cometiendo en la estimación.
Estimación del error
La estimación del error o la variabilidad de los resultados entre muestra y muestra la haremos por simulación. En concreto, supongamos que los porcentajes reales fueran conocidos y tales que \(\pi_A=0.60\) y \(\pi_B=0.40\). Podríamos simular una encuesta seleccionando 100 respuestas al azar de manera que cada respuesta sea A o B de acuerdo a las proporciones anteriores. Si repetimos esto 1000 y hacemos un histograma de los resultados obtendríamos:
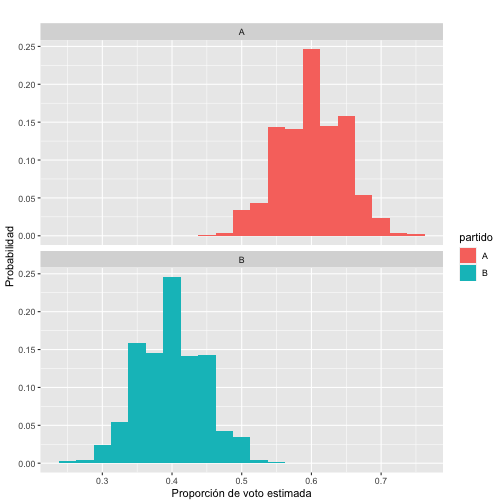
Lo que puede verse en esa gráfica es que la mayoría de las estimaciones quedan cerca del valor real, pero que también existe cierta variabilidad en las estimaciones. Podríamos dar un rango de valores (o intervalo) que contenga el 95% de los valores estimados en cada muestra. Para el partido A sería (0.51, 0.69) y para el partido B sería (0.31, 0.49).
Como puede verse, ambos intervalos aparecen centrados en los valores reales y la amplitud es de dos veces \(0.10\). Este valor es lo que reportaríamos como error. Este valor viene a decir que en el 95% de las encuestas que hagamos, el valor real de la proporción va a estar, como mucho, a \(0.10\) del valor real de la proporción de votantes.
Conviene comentar que este error es conocido desde hace mucho tiempo por los matemáticos y va a ser igual a
\[1.96 * \sqrt{\frac{\pi (1 - \pi)}{n}}\]donde \(n\) es el número de encuestas recogidas y \(\pi\) la proporción real que estamos intentando estimar. Como \(\pi\) es desconocida en la práctica se suele tomar una cota superior de este error dada por
\[1.96 * \sqrt{\frac{0.5 * (1 - 0.5)}{n}}\]Para las 100 encuestas (es decir, \(n = 100\)) que hemos hecho en las simulaciones el error estimado sería de 0.098, que se parece mucho al error que aparece en las simulaciones.
Encuestas a las elecciones municipales en Albacete el 24M
En la práctica tendremos una situación en la que hay varios partidos con porcentajes de voto muy distintos. Los resultados de las elecciones municipales en Albacete del 24 de mayo de 2014 aparecen en la tabla de abajo. También hemos incluído los resultados de las encuestas realizadas por los alumnos de 1ºD y 1ºE de la Escuela de Ingenieros Industriales de Albacete, así como la encuesta publicada por el periódico La Tribuna de Albacete.
| PARTIDO | VOTOS | CONCEJALES | PORCENTAJE | VOTOS ENCUESTA | PORCENTAJE ENCUESTA | CONCEJALES ENCUESTA | PORCENTAJE LA TRIBUNA | CONCEJALES LA TRIBUNA |
|---|---|---|---|---|---|---|---|---|
| PP | 29351 | 10 | 33.48 | 419 | 24.96 | 9 | 38.6 | 11.5 |
| PSOE | 23944 | 8 | 27.31 | 374 | 22.28 | 8 | 24.8 | 7.0 |
| Ganemos | 13446 | 5 | 15.34 | 158 | 9.41 | 3 | 15.7 | 4.0 |
| Cs | 11902 | 4 | 13.58 | 305 | 18.17 | 7 | 16.8 | 4.5 |
| UPyD | 1532 | 0 | 1.75 | 51 | 3.04 | 0 | NA | 0.0 |
| Otros | 7497 | 0 | 8.55 | 372 | 22.16 | 0 | 4.1 | 0.0 |
Como puede verse, se realizaron un total de 1679 encuestas. La muestra se diseño teniendo en cuenta lo siguiente:
-
Se realizó una encuestación en cada uno de los barrios de Albacete
-
El número de personas que debían ser entrevistadas en cada barrio se determinó de acuerdo a la población (según edad y sexo) de cada barrio
-
La recogida de datos se realizó mediante un tablet en la que el entrevistado debía marcar el partido del que prefería que fuera el futuro alcalde de Albacete
Para estimar el error de las encuestas realizadas, podemos repetir el experimento anterior y simular respuestas a las encuestas usando los porcentajes reales de voto para ver cuál sería la variabilidad esperada y compararla con los resultados obtenidos. La siguiente gráfica muestra la variabilidad de acuerdo al número de encuestas realizado, el porcentaje de voto estimado en nuestra encuesta (en negro) y el de La Tribuna (en rojo):
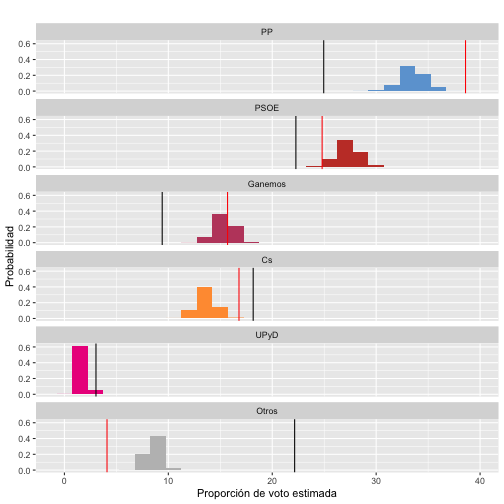
Lo más remarcable es el voto oculto que experimentan PP y PSOE en nuestras encuestas. Las encuestas subestiman el porcentaje de voto real a estos dos partidos, que quedaría englobado en el apartado de OTROS.
Estimación del número de concejales
Una vez que se ha realizado el cómputo de los votos válidos se realiza la distribución de concejales, que para la ciudad de Albacete son 27. Al reparto sólo pueden acceder los partidos que hayan obtenido al menos un 5% de los votos válidos, y éste se realiza de acuerdo a la Ley d’Hont.
La Ley d’Hont establece que el reparto ha de hacerse de acuerdo una serie de puntuaciones que se calculan dividiendo el número de votos obtenido (o el porcentaje) desde 1 hasta el número total de concejales. Luego estos coeficientes se ordenan de mayor a menor y los concejales serían asignados a los partidos con las 27 puntuaciones mayores (por ser ese el número de concejales en Albacete).
Para el caso concreto de Albacete, la siguiente tabla muestra las puntuaciones según el número real de votos obtenido:
| PP | PSOE | Ganemos | Cs | UPyD | |
|---|---|---|---|---|---|
| Nº votos/1 | 29351 |
23944 |
13446 |
11902 |
1532 |
| Nº votos/2 | 14676 |
11972 |
6723 |
5951 |
766 |
| Nº votos/3 | 9784 |
7981 |
4482 |
3967 |
510.7 |
| Nº votos/4 | 7338 |
5986 |
3362 |
2976 |
383 |
| Nº votos/5 | 5870 |
4789 |
2689 |
2380 | 306.4 |
| Nº votos/6 | 4892 |
3991 |
2241 | 1984 | 255.3 |
| Nº votos/7 | 4193 |
3421 |
1921 | 1700 | 218.9 |
| Nº votos/8 | 3669 |
2993 |
1681 | 1488 | 191.5 |
| Nº votos/9 | 3261 |
2660 | 1494 | 1322 | 170.2 |
| Nº votos/10 | 2935 |
2394 | 1345 | 1190 | 153.2 |
| Nº votos/11 | 2668 | 2177 | 1222 | 1082 | 139.3 |
Se han marcado las 27 puntuaciones más altas que son las que proporcionan algún concejal. UPyD no participa en el reparto de concejales porque no ha llegado al mínimo del 5% de los votos válidos. Aun así, vemos que hubiera quedado muy lejos de obtener un concejal en caso de haber entrado.
Como última puntualización al reparto de concejales, este sistema electoral no proporciona un reparto de concejales proporcional al porcentaje de votos obtenido, sino que tiene a favorecer a los partidos más votados.
Igual que hemos hecho con los porcentajes de voto, también es posible estimar cuántos escaños obtendría cada partido por simulación. La gráfica que aparece a continuación muestran el número de escaños que obtendríamos con las simulaciones de las encuestas (usando los porcentajes de voto reales), el que obtuvimos con nuestas encuestas (en negro) y el publicado por el periódico La Tribuna de Albacete (en rojo). Como puede verse, en general nuestros resultados no estaban muy alejados de los resultados reales pero sí que quedaban fuera de lo deseable.
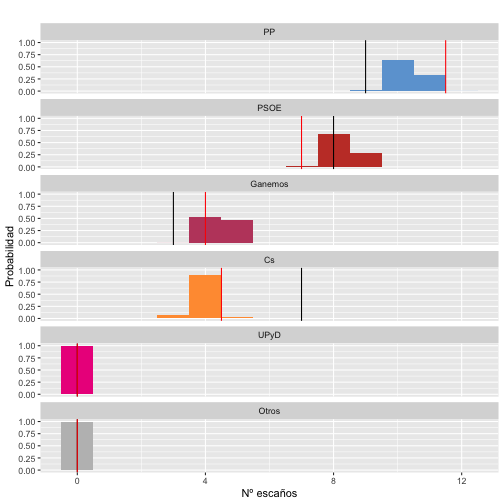
Como nuestras encuestas sobrestimaron el número de votos a Ciudadanos este partido parece obtener un número de escaños mucho mayor de los que en realidad tuvo. Para el resto de partidos los resultados sí que fueron bastante cercanos, aunquefuera de lo que cabría esperar por la variabilidad del muestreo. Los resultados de la encuesta del periódico La Tribuna cayeron dentro de lo que cabría esperar de acuerdo al error esperado e incluso parece que afinaron más que en nuestra encuesta.
Agradecimientos
Este trabajo no se habría llevado a cabo sin el entusiasmo y la colaboración de Mario Plaza Delgado, que es el verdadero impulsor del desarrollo de las encuestas. También hay que agradecer a los alumnos de 1ºD y ºE del Grado en Ingeniería Industrial del curso 2014-2015 por participar en la recogida de encuestas. La Escuela de Industriales de Albacete y el Departamento de Matemáticas de la UCLM también aportaron medios económicos para poder llevar a cabo las encuestas.