Predicción de escaños en las elecciones andaluzas del 2D usando encuestas provinciales y regionales
Análisis Bayesiano de las encuestas de las elecciones andaluzas del 2D
Predicción de escaños a partir de varias encuestas regionales y provinciales
Virgilio Gómez Rubio
Departamento de Matemáticas
Universidad de Castilla-La Mancha
Campus de Albacete
Introducción
En este análisis de las encuestas sobre las elecciones andaluzas del 2 de diciembre de 2018 usamos un modelo jerárquico Bayesiano para combinar la información de las encuestas regionales y provinciales. El objetivo es usar toda la información disponible para mejorar la predicción de escaños sin importar la escala geográfica a la que se hayan hecho la encuestas.
Métodos
De manera similar a los artículos anteriores, hemos considerado encuestas de intención de voto para intentar predecir el número de escaños. Los datos que hemos utilizado son los mismos que en los dos análisis anteriores y no se reproducen aquí..
Para modelizar las encuestas a nivel regional, se utiliza un modelo jerárquico Bayesiano multinomial-Dirichlet.Esto nos modeliza el porcentaje de votos total para cada partido. Además, usaremos un modelo multinomial para modelizar los resultados de las encuestas por partido y provincia. A nivel provincial, se ha supuesto que la probabilidad de votar a un partido en una determinada provincia depende del porcentaje global de voto de cada partido modificado por un efecto aleatorio para cada provincia y partido. Esto hace que los porcentajes de votos a un determinado partido en cada provincia se parezcan a los globales pero que también haya margen para variaciones locales. Para más detalles, se puede ver el modelo de WinBUGS más abajo.
Hemos usado el paquete rjags para ajustar el modelo Bayesiano usando este código:
model {
for(i in 1:n.encuestas.prov) {
for(j in 1:n.provincias) {
votos.prov[i, j, 1:n.partidos] ~ dmulti(p.prov[j, 1:n.partidos], n.prov[i, j])
}
}
for(j in 1:n.provincias) {
for(i in 1:n.partidos) {
log(phi[j, i]) <- log(p[i]) + u[j, i]
p.prov[j, i] <- phi[j, i]/sum(phi[j,])
u[j, i] ~ dnorm(0, tau)
}
}
tau ~ dgamma(a0, b0)
for(i in 1:n.encuestas.ca) {
votos.ca[i, 1:n.partidos] ~ dmulti(p[1:n.partidos], n.ca[i])
}
p[1:n.partidos] ~ ddirch(alpha[1:n.partidos])
}
A la hora de ajustar el modelo usando simulación MCMC hemos usado 5000 iteraciones de calentamiento y otras 10000 para obtener las estimaciones de los parámetros. A la hora de generar estas simulaciones, nos hemos quedado con 1 de cada 10 simulaciones para disminuir la autocorrelación. Además, con cada una de estas 10000 simulaciones hemos estimado el número de escaños que correspondería a cada partido para obtener una simulación de los escaños por provincias y totales.
Resultados
Para dar una medida de la variabilidad de esta estimación, hemos usado los resultados de las simulaciones para estimar el número de escaños totales que cada partido obtendría. Para ello hemos usado los porcentajes estimados en cada iteración y calculado los escaños. Posteriormente, hemos calculado una serie de estadísticos resumen con los escaños obtenidos por cada partido.
Aquí vemos los estadísticos resumen:
| PP | PSOE | Adelante | Cs | Vox | |
|---|---|---|---|---|---|
| Min. | 21.00 | 34.00 | 15.00 | 18.00 | 0.0000 |
| 1st Qu. | 25.00 | 39.00 | 19.00 | 21.00 | 0.0000 |
| Median | 26.00 | 40.00 | 20.00 | 22.00 | 0.0000 |
| Mean | 26.19 | 39.72 | 20.32 | 22.27 | 0.4932 |
| 3rd Qu. | 27.00 | 41.00 | 21.00 | 23.00 | 1.0000 |
| Max. | 31.00 | 45.00 | 26.00 | 28.00 | 4.0000 |
Y aquí tenemos un intervalo de credibilidad al 95% para el número de escaños por partido:
| PP | PSOE | Adelante | Cs | Vox | |
|---|---|---|---|---|---|
| 2.5% | 24 | 37 | 18 | 20 | 0 |
| 97.5% | 29 | 43 | 23 | 25 | 2 |
Nuestra metodología parece dar intervalos de credibilidad más estrechos con un nivel de confianza más alto.
La siguiente tabla muestra los resultados por provincias. En concreto, el número más probable de escaños conseguidos, junto con un intervalo de credibilidad al 95% (entre paréntesis).
| Almería | Cádiz | Córdoba | Granada | Huelva | Jaén | Málaga | Sevilla | |
|---|---|---|---|---|---|---|---|---|
| PP | 4 (3 - 5) | 3 (2 - 4) | 3 (2 - 4) | 3 (3 - 4) | 3 (2 - 3) | 3 (2 - 4) | 4 (3 - 5) | 3 (3 - 4) |
| PSOE | 4 (3 - 5) | 5 (4 - 6) | 5 (4 - 5) | 5 (4 - 6) | 5 (4 - 5) | 5 (4 - 6) | 5 (4 - 6) | 7 (6 - 8) |
| Adelante | 1 (1 - 2) | 3 (3 - 4) | 2 (2 - 3) | 2 (2 - 3) | 2 (1 - 2) | 2 (1 - 2) | 3 (3 - 4) | 4 (3 - 5) |
| Cs | 3 (2 - 3) | 3 (3 - 4) | 2 (2 - 3) | 3 (2 - 3) | 2 (1 - 2) | 2 (1 - 2) | 4 (3 - 5) | 4 (3 - 5) |
| Vox | 0 (0 - 1) | 0 (0 - 1) | 0 (0 - 0) | 0 (0 - 0) | 0 (0 - 0) | 0 (0 - 0) | 0 (0 - 1) | 0 (0 - 1) |
El modelo Bayesiano nos combina los datos de las distintas encuestas de manera que se obtiene una estimación de las proporciones de voto mucho más fiable y, por tanto, del número de escaños obtenido por cada partido. La siguiente figura muestra las distribuciones marginales a posteriori de los escaños obtenidos por cada partido. Se han incluido los escaños reales de las elecciones.
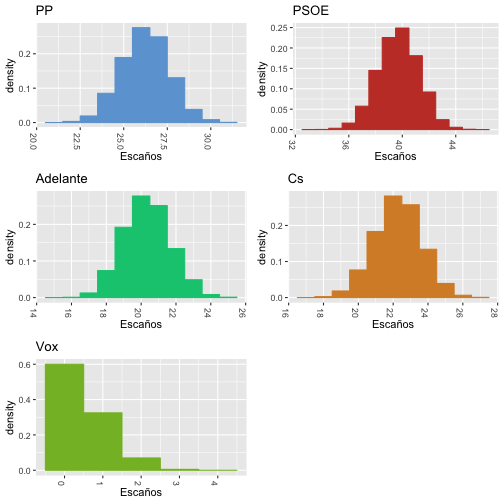
Por último, vamos a mostrar en una gráfica el número de escaños que obtendrían los partidos de izquierdas, junto con el límite de 55 escaños que marca la mayoría absoluta:
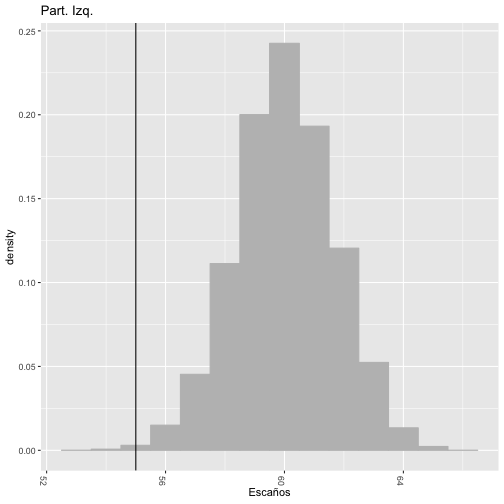
La gráfica indica que los partidos de izquierdas obtendrían una mayoría absoluta con una gran probabilidad.
Conclusiones
Hemos visto cómo los modelos jerárquicos Bayesianos nos permiten combinar datos de diferentes encuestas para poder realizar una estimación del número de escaños que obtendría cada partido en las elecciones andluzas del 2 de diciembre de 2018. Los resultados muestran que los partidos de izquierdas obtendrían una mayoría absoluta en número de escaños con una probabilidad del 99.98%.
Por algún motivo, este modelo proporciona resultados muy similares a los obtenidos usando solamente las encuestas a nivel provincial. Esto puede deberse a que el modelo produce un sobreajuste de los porcentajes de voto a nivel provincial.
Apéndice: Software y datos utilizados
-
R, para el análisis de datos
-
Diversas encuestas publicadas en medios nacionales.