Predicción de escaños en las elecciones vascas del 25S de 2016
Análisis Bayesiano de las encuestas de las elecciones vascas del 25S 2016
Predicción de escaños a partir de varias encuestas
Virgilio Gómez Rubio
Departamento de Matemáticas
Universidad de Castilla-La Mancha
Campus de Albacete
Introducción
En este artículo, escrito a la carrera desde Barajas, hago una predicción de los resultados de las elecciones del 25 de septiembre de 2016 al parlamento vasco.
Métodos
Hemos encontrado referencias a 3 encuestas publicadas en medios de comunicación que recogen la intención de voto a nivel provincial. Queremos combinar estas encuestas para obtener una estimación más precisa de los porcentajes de voto a nivel provincial y, a partir de aquí, obtener una estimación de los escaños obtenidos por cada partido en cada provincia y de ahí sacar el número de escaños totales.
En concreto, las encuestas que hemos considerado en este análisis se han obtenido de diversas webs y se han resumido en una tabla. Los datos son:
| Empresa | Provincia | Dato | N | Error | PP | PSOE | PODEMOS | Cs | PNV | BILDU | OTROSBL |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Metroscopia | Araba | Porcentaje | 500 | 3.5 | 12.2 | 9.5 | 21.5 | 4.6 | 25.9 | 19.7 | 6.6 |
| Bizkaia | Porcentaje | 800 | 4.5 | 9.5 | 12.1 | 17.4 | 1.3 | 41.7 | 15.4 | 2.6 | |
| Gipuzkoa | Porcentaje | 800 | 4.5 | 6.1 | 13.3 | 17.1 | 2.0 | 32.2 | 25.6 | 3.7 | |
| Ikerfel | Araba | Porcentaje | 900 | 3.3 | 14.7 | 13.8 | 20.9 | 2.8 | 28.8 | 17.0 | 2.0 |
| Bizkaia | Porcentaje | 900 | 3.3 | 7.8 | 13.8 | 19.3 | 2.1 | 39.7 | 15.9 | 1.4 | |
| Gipuzkoa | Porcentaje | 900 | 3.3 | 7.7 | 10.9 | 18.7 | 2.1 | 35.2 | 24.6 | 0.8 | |
| SigmaDos | Araba | Porcentaje | 400 | NA | 17.6 | 13.4 | 18.1 | 3.2 | 26.9 | 18.3 | 2.5 |
| Bizkaia | Porcentaje | 400 | NA | 8.7 | 12.0 | 17.3 | 2.1 | 39.6 | 17.2 | 3.1 | |
| Gipuzkoa | Porcentaje | 400 | NA | 7.2 | 12.9 | 15.7 | 1.7 | 31.2 | 28.8 | 2.5 | |
| Ikertalde, GPS Gobierno Vasco | Araba | Porcentaje | 574 | 4.2 | 17.6 | 12.4 | 21.0 | 3.1 | 24.6 | 18.3 | 3.0 |
| Bizkaia | Porcentaje | 1148 | 3.0 | 8.7 | 11.9 | 19.0 | 2.3 | 38.1 | 17.1 | 2.9 | |
| Gipuzkoa | Porcentaje | 854 | 3.4 | 6.2 | 11.1 | 19.1 | 1.6 | 30.0 | 29.5 | 2.5 | |
| CIS, IMOP | Araba | Porcentaje | 1000 | NA | 14.8 | 11.3 | 23.0 | 2.8 | 27.1 | 19.3 | 1.7 |
| Bizkaia | Porcentaje | 1000 | NA | 8.1 | 11.2 | 17.9 | 1.4 | 42.7 | 17.3 | 1.4 | |
| Gipuzkoa | Porcentaje | 1000 | NA | 7.2 | 10.0 | 18.6 | 1.9 | 34.8 | 25.4 | 2.1 |
Algunas de las encuestas muestran ya directamente los escaños estimados para cada partido, con lo que no las hemos incorporado en nuestro modelo.
Usaremos un modelo jerárquico Bayesiano multinomial-Dirichlet para combinar todos los resultados y obtener estimaciones más precisas de las proporciones de voto en cada provincia.
Hemos usado el paquete rjags para ajustar el modelo Bayesiano usando este código:
model {
for(i in 1:n.encuestas) {
for(j in 1:n.provincias) {
votos[i, j, 1:n.partidos] ~ dmulti(p[j, 1:n.partidos], n[i, j])
}
}
for(j in 1:n.provincias) {
p[j, 1:n.partidos] ~ ddirch(alpha[1:n.partidos])
}
}
A la hora de ajustar el modelo usando simulación MCMC hemos usado 5000 iteraciones de calentamiento y otras 10000 para obtener las estimaciones de los parámetros. A la hora de generar estas simulaciones, nos hemos quedado con 1 de cada 10 simulaciones para disminuir la autocorrelación. Además, con cada una de estas 10000 simulaciones hemos estimado el número de escaños que correspondería a cada partido para obtener una simulación de los escaños por provincias y totales.
Resultados
Una vez que hemos ajsutado el modelo, podemos estimar el número de escaños por provincia usando las medias a posteriori de los porcentajes de voto por provincias y partidos:
| Araba | Bizkaia | Gipuzkoa | |
|---|---|---|---|
| BILDU | 5 | 4 | 7 |
| PNV | 7 | 11 | 9 |
| PODEMOS | 6 | 5 | 5 |
| PP | 4 | 2 | 1 |
| PSOE | 3 | 3 | 3 |
Los escaños totales por partidos serían:
| Escaños | |
|---|---|
| BILDU | 16 |
| PNV | 27 |
| PODEMOS | 16 |
| PP | 7 |
| PSOE | 9 |
Para dar una medida de la variabilidad de esta estimación, hemos usado los resultados de las simulaciones para estimar el número de escaños totales que cada partido obtendría. Para ello hemos usado los porcentajes estimados en cada iteración y calculado los escaños. Posteriormente, hemos calculado una serie de estadísticos resumen con los escaños obtenidos por cada partido.
Aquí vemos los estadísticos resumen:
| PP | PSOE | PODEMOS | Cs | PNV | BILDU | |
|---|---|---|---|---|---|---|
| Min. | 6.000 | 8.000 | 13.00 | 0.0000 | 25.00 | 14.00 |
| 1st Qu. | 7.000 | 9.000 | 15.00 | 0.0000 | 27.00 | 16.00 |
| Median | 7.000 | 9.000 | 16.00 | 0.0000 | 27.00 | 16.00 |
| Mean | 7.279 | 8.956 | 15.56 | 0.1408 | 27.08 | 15.98 |
| 3rd Qu. | 8.000 | 9.000 | 16.00 | 0.0000 | 27.00 | 16.00 |
| Max. | 9.000 | 10.000 | 17.00 | 1.0000 | 29.00 | 18.00 |
Y aquí tenemos un intervalo de credibilidad al 95% para el número de escaños por partido:
| PP | PSOE | PODEMOS | Cs | PNV | BILDU | |
|---|---|---|---|---|---|---|
| 2.5% | 7 | 8 | 14 | 0 | 26 | 15 |
| 97.5% | 8 | 9 | 16 | 1 | 28 | 17 |
El modelo Bayesiano nos combina los datos de las distintas encuestas de manera que se obtiene una estimación de las proporciones de voto mucho más fiable. La siguiente figura muestra las distribuciones marginales a posteriori de los escaños obtenidos por cada partido:
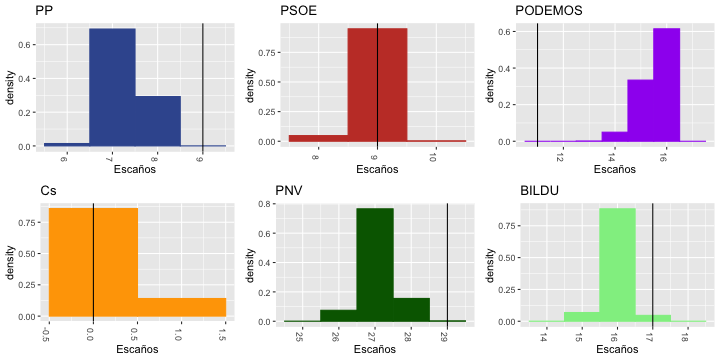
La gráfica indica que los partidos nacionalistas obtendrían una mayoría absoluta con una gran probabilidad. La línea vertical muestra el resultado real de las elecciones.
Apéndice: Software y datos utilizados
- R, para el análisis de datos
- Electograph, como fuente de datos de encuestas